1. Introduction to Time and Space
Definitions
Consider there is a turing machine M with alphabet Σ, and g is a function N → N, we say M runs in time g and runs in space g with at most g(|x|) steps and g(|x|) squares with a finite x many Strings. If there is a language L over some alphabet, we say L runs in Time(g) and Space(g) such that there is a deterministic turing machine M recognizing L runs in time and space g. In another words, this is the definition of time and space complexity in a turing machine view.
Linear ‘Speed-up’ theorem
There is a theorem about complexties: Let f be a function f: N → N, and c > 0, we could get
$$Time(f(n)) ⊆ Time(c · f(n) + n)$$ $$Space(f(n)) ⊆ Space(c · f(n))$$
In an exmaple, we don’t have to write Time(5x² + 4x + 3), instead, we could write Time(n²).
Categories of Time and Space
Consider a G which includes a set of functions N → N: $$Time(G) = \bigcup_{g ∈ G} Time(g)$$ $$Space(G) = \bigcup_{g ∈ G} Space(g)$$
We could have some handy functions:
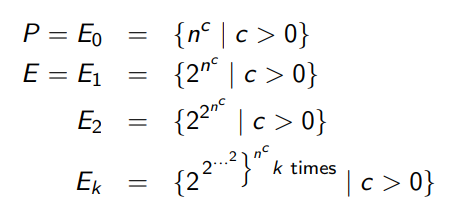
In this graph, P is denoted as E0, which means some Polynomial equations. And E here means Exponential equation denoted as E1 to Ek, where Ek is a generalised form.
By combining the idea of G and those handy functions, we could define some Time and Space categories:

Note: The reason why we don’t have Time(log n) is because a Turing Machine which can only operate in time log n can’t even read the input. So we don’t care about this case.
More Definitions
If L is a language over some alphabet and g is a function N → N, we say that L is in NTime(g) and NSpace(g) if there is a turing machine M recognizing L such that M runs in time g. So in this case, the difference between NTime(g) and Time(g) is only the turing machine is deterministic or not.
Let’s look at an example:

This is a reachability problem, which focus on directed graph, here lets look at a pseudo-code solving this problem.

The three input parameters G, u, and v means the directed graph, start node and the end node. This algorithm use a parameter c to manage the count of viewed nodes. In the while loop, the algorithm randomly choose a node w’, which is either same as w or there is an edge between w and w’. If there is no more such nodes or w is equal to v, the while loop breaks, and we test if c is less than n to identify which case is happening from above.
It is clear that this algorithm is non-deterministic (For every states, there might be more than one possible next states). And because we only have to maintain a count number c, which takes log n space in bits, so this problem could be solve in NLogSpace.
2. Inclusions
Here we discuss the inclusion(relationship) between complexities.
For all the complexities we’ve learned so far, we could concludes some inclusions:
$$Time(G) ⊆ NTime(G)\quad\quad Space(G) ⊆ NSpace(G)$$ $$Time(G) ⊆ Space(G)\quad\quad NTime(G) ⊆ NSpace(G)$$
And also, if the set of functions G ⊆ another set of functions H, then $Time(G) ⊆ Time(H)$, and similarity for NTime, Space and NSpace.
Configuration Graph
Consider a turing machine M = $\langle K, Σ, Q, q0,T \rangle$, suppose for every tapes in the turing machine, the maximum amount of space used is s(n). In this case, the maximum amount of configurations to be considered is:
$$|Q| · |Σ|^{K·s(n)} · (s(n) + 1)^K ∈ 2^{O(s(n))}$$
We called this set of configurations as V. Now try think in the perspective of a directed graph, we could transform the set V into a directed graph $G = (V, E)$, where in this graph $(c, d) ∈ E$ means any transitions from c to d(states change inside a turing machine).
We could identify a start configuration $c_0$ (with input x) and a success configuration $c_*$. If M accepts x, it means there is a path from start node $c_0$ to $c_*$.
Derivation 1
Let’s look at a theorem:
$NSpace(g) ⊆ Time(2^{O(g)})$
Let a language L be in $NSpace(g)$, we need to prove that it is also in $Time(2^{O(g)})$.
Suppose there’s a input n, we build a configuration graph based on this input. Because of $|G| < 2^{O(g(n))}$, and we could search a path in G from starting node to success node in a linear G time, the theorem is proved.
Corollary
From the above derivation, we could conclude that
$$NLogSpace ⊆ PTime, NPSpace ⊆ ExpTime$$ $$NExpSpace ⊆ 2-ExpTime, etc.$$
Derivation 2
Another theorem here:
$NTime(g) ⊆ Space(g)$
Let a language L in $NTime(g)$, we need to prove that it is also in $Space(g)$.
Consider a non-deterministic turing machine M runs in Time(g), then M could make at most $g(n)$ non-deterministic choices, for each choice we could represent by $k_{g(n)}$, and for entire list of choices, the representation is $k_1 … k_{g(n)}$.
In this case, imagine there is a deterministic turing machine $M^*$ which runs in Space(g) just like M above, but on the basis of M, add an extra new tape to record all non-deterministic choices, expressed as a string $k_1 … k_{g(n)}$. Now, the turing machine could easily iterate all possible configurations without using extra space, and so the theorem is proved.
Corollary
From the above derivation, we could conclude that
$$LogSpace ⊆ NLogSpace ⊆ PTime ⊆ NPTime ⊆$$ $$PSpace ⊆ NPSpace ⊆ ExpTime ⊆ NExpTime ⊆$$ $$ExpSpace ⊆ NExpSpace ⊆ 2-ExpTime…$$
3. A Separation Result
In the last blog introducing turing machine, we discussed about the Halting problem (review here), which we get the result that halting problem is an undecidable problem. Now, let’s have a look at the f-bounded Halting problem:

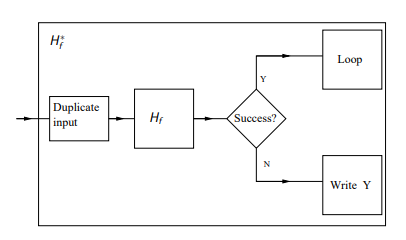
Suppose $HALTING_f$ is recognized by a Turing machine $H_f$, guaranteed to terminate in $Time(f(\lfloor n/2 \rfloor))$, by using the proving method in last blog, we could get a conclusion:
$$HALTING_f \notin Time(f(\lfloor n/2 \rfloor))$$