Propositional Logic Satisfiability
Definitions
We call $P = \lbrace p_1, p_2, … \rbrace $ as propositional letters. Every element in $P$ is a formula. If $\psi_1$ and $\psi_2$ are formulas, then the following equations are formulas, too.
$$(¬\psi_1), (\psi_1 ∨ \psi_2), (\psi_1 ∧ \psi_2), (\psi_1 → \psi_2)$$
An assignment is a function $\theta: P → \lbrace T, F\rbrace$, for example:
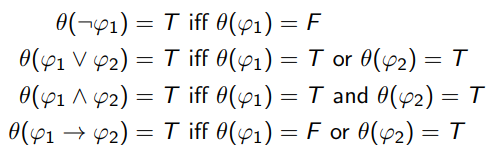In a simple way, an assignment is like a machine running a logic equation and excute a result. A formula $\psi$ is satisfiable if there is a formula $\theta$ such that $\theta(\psi)=T$.
A literal is an expression $p$ or $\neg p$, where $p$ is a propositional letter.
A clause is a combination of literals, for example:
$$p1 ∨ ¬p2 ∨ p3$$
$$¬p1 ∨ ¬p4 ∨ ¬p7 ∨ p8$$
$$¬p14$$
$$p1$$
$$⊥$$
We could also denote the opposite of a literal $\ell$ by $\overline\ell$.
We use $\gamma$ to represent a clause and $\Gamma$ to represent a set of clauses. A set of clauses is satisfiable if there is an assignment equals to $T$ for all $\gamma ∈ \Gamma$ (All clauses needs to be true!!).
SAT & k-SAT Problem
Here we can define two problems: SAT and k-SAT
The Davis-Putnam (-Logemann-Loveland) algorithm could solve the SAT problem:
As we want to test satisfiability, we need to know the truth of each single clauses in the set $\Gamma$. The resolve function could simplify $\Gamma$ by assuming a clause is true, bring this true clause to the whole set, eliminate all true clauses (a clause is true if our assumed clause is in) and delete any $\overline\ell$. You might be confused now, but let’s move on to main body part of this algorithm and it might solve your confusion. First, we check if $\Gamma$ is empty or contains an empty clause to return true or false base on the case, then for any unit clause(single literal) in $\Gamma$, call resolve() to do simplification. There are few conditions here: If resolve() returns an empty $\Gamma$, we return a Yes because all clauses are true and eliminated by resolve(), but if the returned $\Gamma$ is not empty and it contains an empty clause, we return a No because all $\overline\ell$ are eliminated in that empty clause which results in a false. If it is not the above two situations, it means that we still have a literal that has not appeared before, so now we call it recursively the DPLL() two times, each time the input would be the union of $\Gamma$ and the first literal in the first clause (positive and negative), this literal will be the unit clause in the recursion, and so on we could do furthur elimination and finally get the result.