What is NLU?
In the previous blogs I mainly focused on NLP, which refers to processing unstructured data(texts) into structured data by tokenization, lemmatisation, stemming, etc. NLU will more focus on making sure the initial meaning of language and let the machine recognize it while understanding the changes within texts.
Such applications of NLU could be make the answers of chatbot more natural like human reaction, it could make machines more intelligent.
NLU tasks could be generalized into 4 types:
- Sequence classification
- Pairwise sequence classification
- Sequence labelling
- Span based operations
Word Representation
Here we will introduce a new type of word embedding method, other embedding methods like this could be viewed from this link: Natural Language Processing - Text Representation.
PMI(Pointwise Mutual Information) measures how often a target word $w$ and a context word $c$ co-occur, compared with when they occur independently. The math representation is like this:
$$PMI(w, c) = \log_2 \frac{P(w, c)}{P(w)P(c)}$$
PPMI(Positive Pointwise Mutual Information), which is drawn from the PMI, replaces all negative values with 0 of the PMI result. It is more often used than PMI, one of the reason is that it performs better with sparse data. PMI has a negative value when calculating the probability of co-occurrence, while PPMI solves this problem by setting all values less than or equal to zero to zero, making the results easier to interpret. In addition, PPMI is able to highlight high frequency co-occurrence pairs while ignoring low frequency co-occurrence to better capture the correlation between words. The math expression is like this:
$$PPMI(w, c) = max(\log_2 \frac{P(w, c)}{P(w)P(c)}, 0)$$
Here is an example of PPMI:
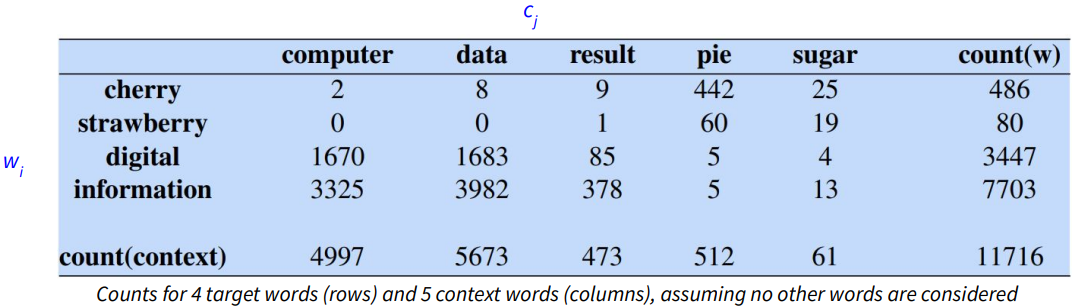
Let’s calculate $PPMI(information, data)$ for the above example. First of all, we need to know the value for $P(w, c)$, $P(w)$ and $P(c)$. The equation for $P(w, c)$ is here:
$$P_{ij} = \frac{f_{ij}}{\sum_{i=1}^{W} \sum_{j=1}^{C} f_{ij}}$$
where we use the number of two words occurrences divided by the overall words. In this case, the result is $3982/11716 = 0.3399$. Then, for $P(w)$ and $P(c)$, we just need to use the occurrences of each word to divided by the overall word count. In this case, $P(w) = 7703/11716 = 0.6575$, and $P(c) = 5673/11716 = 0.4842$.
Hence, the $PPMI(w, c)$ is then:
$$PPMI(information,data) = max(log2(0.3399/(0.6575*0.4842)), 0) = 0.0944$$
Dense Vectors
An introduction to word2vec(Skip-gram & CBOW) and GloVe has been made in this link Natural Language Processing - Word Senses. In this blog we will have a look at fastText.
FastText
FastText is a text processing technique capable of handling unknown words by utilizing subword notation, a set of elements made up of the various N-grams that make up a word. For example, for the word “eating”, it can be broken down into n-grams such as <ea, eat, ati, tin, ing, ng>. fastText works by learning the skip-gram model for each n-gram and representing the word as the sum of the embeddings of the individual N-grams that make up it. So even for a word like “eataly,” the embedding vector is still able to capture the meaning of “eat.”
Sparse VS. Dense Vector
In a sparse vector, each dimension (element) corresponds to either: a document in a large corpus (in a term-document matrix, e.g., in TF-IDF) a word in the vocabulary (in a term-term matrix, e.g., in PPMI). Sparse vectors can have a large number of dimensions (e.g. 10K+) with most values equals to 0, while dense vectors have around hundreds (e.g., 100-500) Models (trained to predict words) are required to learn far fewer weights
By having embeddings, we could achieve more goals like: detecting word similarities, identifying most related words, clustering and visualization, etc.