Cyber Security - Cryptography

In order to keep messages secure, they are two measures, one is two prevent the messages is access by un-authorized party, and another one is, secure messages so that even the message is leaked, the attacker couldn’t understand the message, and this is achieved by cryptography.

Introduction To Cryptography

Cryptography is a crucial part of cybersecurity toolbox, which could be applied to various properties and services, for example:

• Confidentiality (secrecy, privacy) of data in transmission & in storage.
• Integrity of data (data authentication/authenticity) in transit & in storage.
• Authentication of an identity (entity authentication).
• Credential systems (a proof of qualification or competence of a person).
• Digital signatures.
• Electronic money (cryptocurrency, bit coins)

We use ciphers or cryptographic primitives to be building blocks to construct security methods or protocols. There are some examples of the cryptographic algorithms or cryptographic building blocks, such as:

• Symmetric ciphers: The same key is used to encrypt and decrypt the message, and plaintext and the ciphertext have the same size. e.g. DES, AES, one-time pad (Block Ciphers & Stream Ciphers)
• Asymmetric ciphers: RSA, DSA and DH (different keys are used)
• Hash and MACing functions: e.g. SHA256, AES-CBC

We could use these building blocks to construct cryptographic methods and protocols, examples are:

• Modes of encryptions, e.g. CBC (Cipher Block Chaining) mode, CTR (Counter) mode.
• HMAC message authentication code.
• Key distribution/agreement protocols.
• IPSec protocol, SSL, …

Block Cipher

As we said above, block cipher is the basic building components of cryptographic methods and protocols, the following structure demonstrates the basic structure of a block cipher. 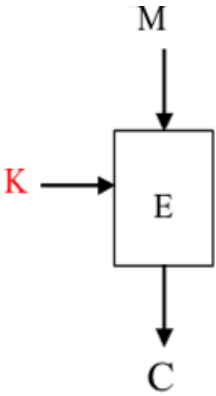In this picture, $M$ and $C$ represents plaintext block and cipher text block respectively, and $K$ is a secret (either a symmetric key or a private key). And the $E$ in the middle represents some encryption methods, where combines with $K$ it becomes $E_K(.)$ ($.$ represents input of the function). Therefore this picture demonstrate a process of encryption, where we input some plaintext and a key, processed by an encryption method, and we could get the cipher text.

Note that if we want to decrypt the cipher text, we need to have a decryption function. The math expression for both encryption and decryption is: $$C = E_K(M)\ (or\ C = E(K, M))$$ $$M = D_K(C)\ (or\ M = D(K, C))$$

Design of Block Cipher

When we design the block cipher, we have to achieve the following three aspects:

1. Completeness Each bit of the output should depend on every bit of the input and every bit of the key. The purpose is that, even two plaintext is similar and only different with one bit, their cipher text should be completely different.

2. Avalanche effect This is to say, if we change one bit in plaintext, the cipher text should change a lot, this prevent analyzing with changing the plaintext and observer the difference.

3. Statistical independence The relationship between plaintext and cipher text should be complex and not linear, even if the attackers got lots of plaintext and cipher texts examples, they can not observe obvious patterns from them.

A good, secure block cipher should have two key properties: confusion and diffusion, where diffusion could achieve Avalanche effect and confusion could achieve Statistical independence. We could achieve these two properties by some round functions(repeat simple functions many times), some examples of simple operations could be substitutions, permutations, XOR, modular multiplication ().

Feistel Block Cipher

The Feistel block cipher is first announce by Horst Feistel in 1970, uses his idea of round function. A graph of the structure is shown below. 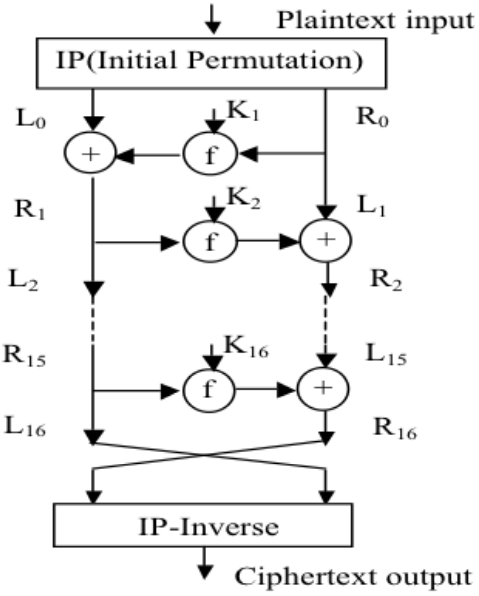The Feistel block cipher will split plaintext into block size of plaintext and do encryption & decryption on each of them. At the beginning, we have a initial permutation for plaintext, this is a non-encrypted pre-processing step that scrambles the data. Then we split them into left ($L$) and right ($R$) part, in each round, we perform round functions represent by $f$ and a key $K$ added to either calculate with left or right part. There are a total of $r$ rounds, for DES, $r$ is equals to 16. After all the calculations are done, we need one more operation which is to inverse the initial permutation to get the original permutation. We could use math to represents this block cipher:

Plaintext = (L0, R0)

For 1 <= i <= r
    Li = Ri-1
    Ri = Li-1 xor f(Ri-1, Ki)
Subkeys Ki is derived from key K
Cipher text = (Rr, Lr) 

Here is a graph with the decryption added: 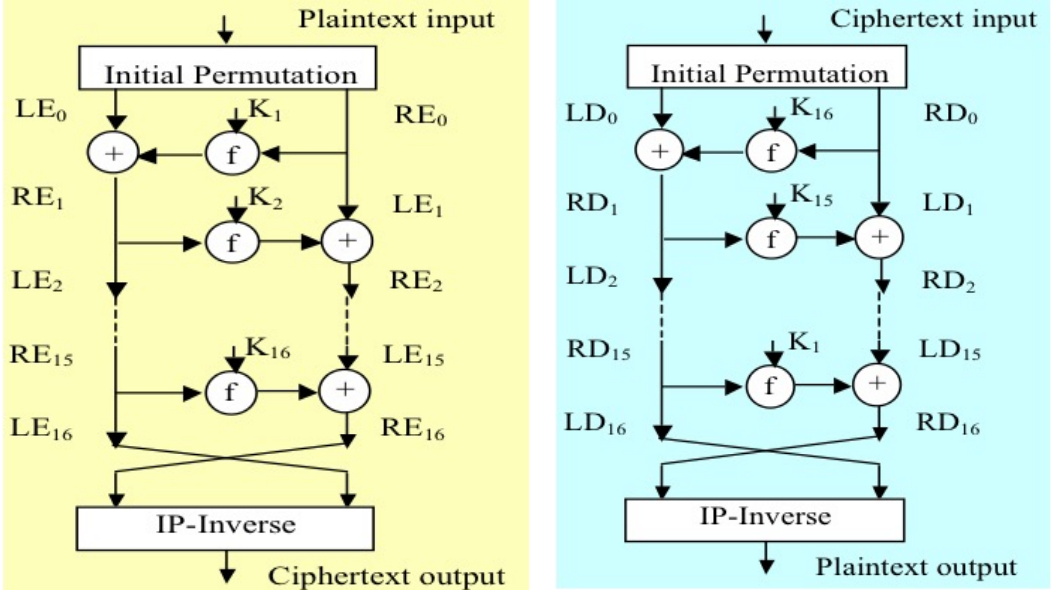For the decryption, we just need to reverse our operations and perform on cipher text. First, perform the same initial permutation as the encryption does, and use the inverse round function with the inverse sequence of key ($K_{16}, K_{15}, …, K_{1}$) to undo the 16 rounds of calculations in encryption, and in the last, undo the initial permutation for itself.

Here are some more explanations to each variables in Feistel block cipher:

• Round function $f$:
  Typically use permutations, substitutions, modular arithmetic.
  Takes a $n$-bit block and outputs a $n$-bit block.
  Each use of the round function employs a different subkey derived from K.
• Block size $n$
  larger block sizes mean greater security but make encryption & decryption slower. Typically $n$ is 128-bit or 256-bits.
• Key size $s$
  larger key size means greater security but reduced speed, a 128-bit size has become a norm.
• Number of rounds $r$
  Typically 10+ rounds

DES

We have mentioned DES need 16 rounds of calculation, but what is DES? It is actually stands for Data Encryption Standard, first published in 1977 as a US Federal Standard, and it is also international standard for banking security. The DES is a Feistel block cipher specified multiple standards on variables of Feistel block cipher. For example, the block size is 64 bits, the key $K$ is 56 bits (actually 8 bytes, but the 8th bit in each byte is a $parity-check bit$), the subkeys $k_1, k_2 , … , k_{16}$ are each 48-bits, generated from key $K$.

DES has some weakness, the 56-bit key is a bit problem - it could be broken on average in $2^55$ trials (brute force attack), a diagram below demonstrate how long can someone broken the DES based on the speed.

Trials	Time Required
1	10^9 years
10^3	10^6 years
10^6	10^3 years
10^9	1 year
10^12	10 hours
Therefore, for the computer nowadays, we need at least 128 bits. Based on this we have some improvements on DES, where Triple DES and AES is invented.

Triple DES

The Triple DES uses two or three DES keys, we call the DES with two keys EDE2 and EDE3 for DES with three keys.

EDE2’s equation is ($K1$ is the first key and $K2$ is the second key): $$C = E_{K1} (D_{K2} (E_{K1} (M)))$$

The key length is now 112 bits, which is more complex than 56-bit keys. Note that if $K1$ equals $K2$, the EDE2 will be same as single DES, as the decryption method will un-do the first encryption.

The EDE3’s equation is: $$C = E_{K3} (D_{K2} (E_{K1} (M)))$$ where each key is 168 bits long.

AES

AES is also a symmetric cipher, which its block size is 128 bits, and key lengths are 128, 192 or 256 bits, based on the key lengths, we name them as AES-128, AES-192 and AES-256. AES uses substitution-permutation methods involving r rounds, where r equals 10, 12 and 14 for different key lengths respectively.

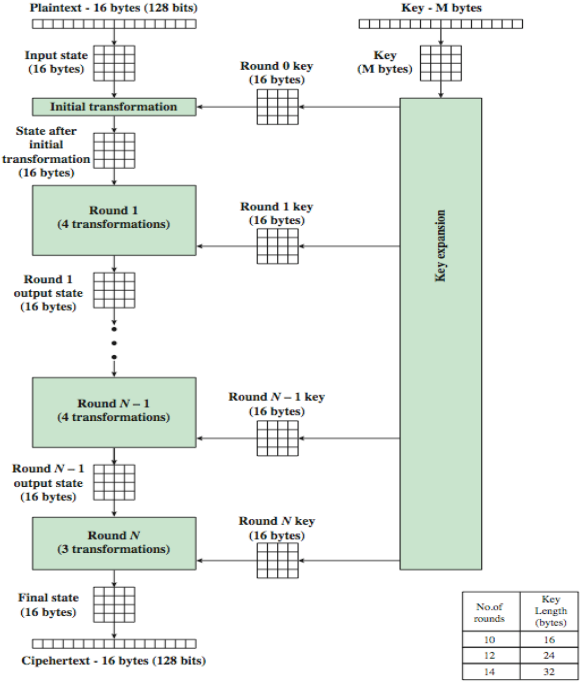
The AES operate on bytes, the 128-bits plaintext will be transformed into a 4 x 4 input matrix, it is called input states. The input state will have a initial transformation, and in each following round, we will do 4 transformations to the state, except for the last round, where we only have three transformations. Moreover, don’t forget about the key. The key is also transformed into a matrix, and processed by a stage called key expansion, where we focus on making the key non-linear, but it doesn’t need to be reversible. In each round we will add the key, doing combination with the input states. This is just an overview of AES, we will look at the details step by step.

Input State

Because AES has a fixed length of block size of 128-bits (16 bytes), and in the most common encoding method a letter is 8 bits (1 byte), if out input plaintext is “ABCDEFGHIJKLMNOP”, it will be transformed into the matrix and processed by ASCII encoding.

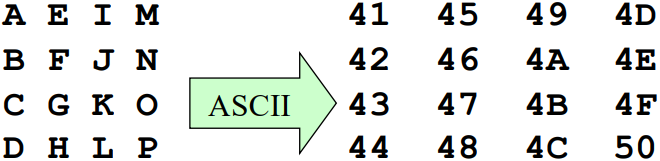
Then, we comes to the step doing the 4 transformations, a basic structure is like this:

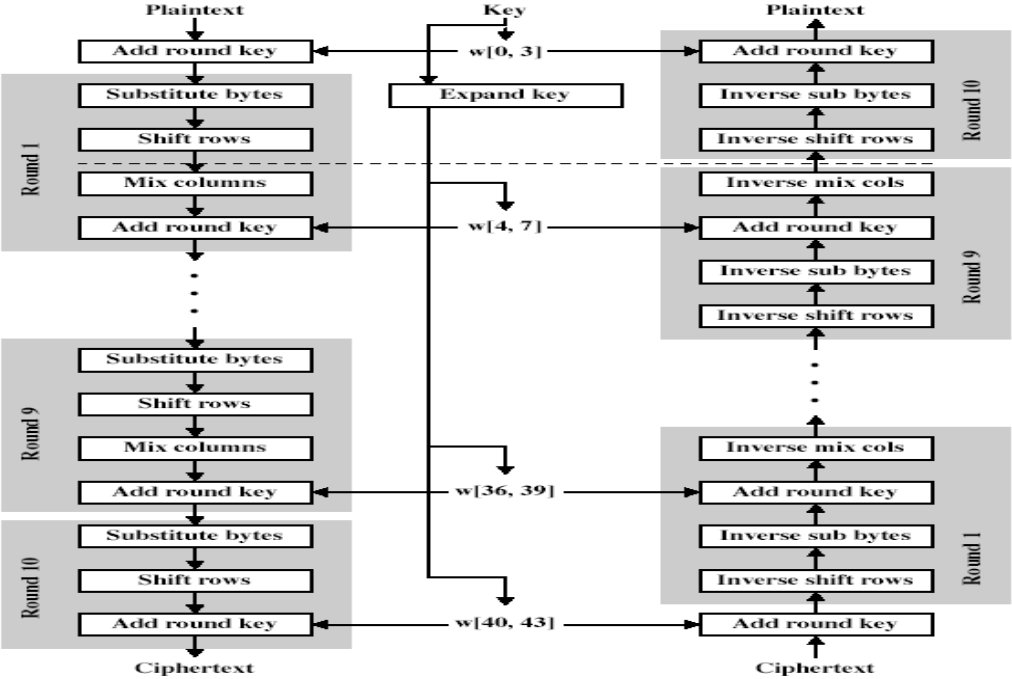
The four transformations are:

1. Substitute Bytes
2. Shift Rows
3. Mix Columns
4. Add Round key

Let’s talk about it one by one.

Substitute Bytes

In substitute bytes, we have a simple table which we call it S-box, used for us to do look-up operations. S-box is a 16 x 16 matrix of byte values, it contains all possible 256 8-bit values. In order to do transformation, we take out the input state, which is a 4 X 4 matrix with a hexadecimal representation in each cell, take the left half(4 bits) of it to determine the x value in S-box, and the right half(4 bits) to determine the y value in S-box. For example, if the cell is ‘83’, then we use 8 as x and 3 as y(In hexadecimal representations, each letter or number is 4 bits).

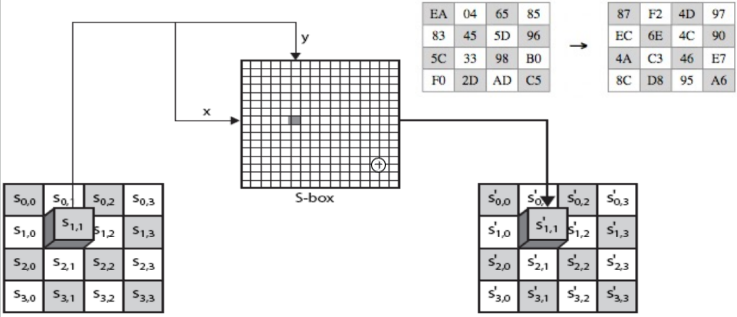
Shift Rows

The shift rows transformation is a simple permutation (circular byte shift), the first row of 4 x 4 matrix doesn’t change, the second row does a 1-byte circular left shift, the second row does a 2-byte circular left shift, and the third row does a 3-byte circular left shift. The decryption process inverse the left shift to right shift. An visual representation of this operation is as below.

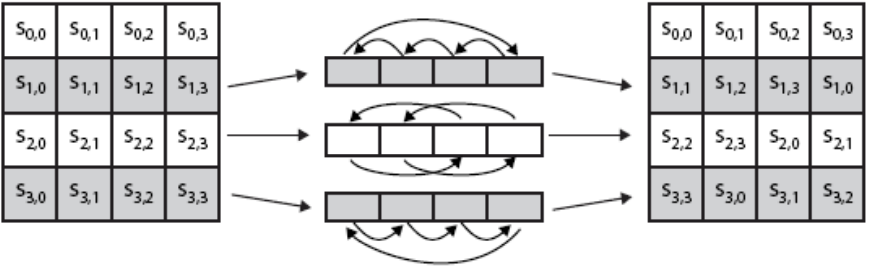
Mix Columns

The mix columns is done by polynomial multiplication in the finite field, in this step, we treat our input in forms of $$a_{n-1}, a_{n-2} , … , a_1, a_0$$ and we express them like this: $$f(x) = a_{n-1}x^{n-1} + a_{n-2}x^{n-2} + … + a_1x + a_0$$ Note that arithmetic follows the ordinary rules of polynomial arithmetic using the basic rules of algebra, with the following two refinements:

1. Arithmetic on the coefficients is performed modulo p (when p = 2, addition and subtraction are done by bitwise XOR)
2. If a multiplication result is a polynomial of degree greater than (n-1), then the polynomial is reduced by modulo some irreducible polynomial m(x) of degree n, i.e., divide it by m(x) and keep the remainder.

Add Round key

The add round key is achieved by using bitwise XOR for the 128-bits state and 128-bits key, as this is easy, we just skip the example.

Pseudo Code

Now, below is the pseudo code for both encryption and decryption. Because all of the four operations are reversible, therefore we just apply the inverse form to undo all transformations.

Now, we could compare DES and AES and list some of their characteristics:

DES	AES
Substitution-Permutation	Substitution-Permutation
iterated cipher, Feistel structure	iterated cipher
64-bit block size	128-bit block size
56-bit key size	128/192/256-bit key sizes
8 different S-boxes	1 S-box
design optimized for hardware implementations	design optimised for byteorientated implementations
closed (secret) design process	open design and evaluation process

N-bit block cipher permutes over $2N$ inputs, so the larger the $N$ value, the longer it takes to attack, thus the more secure the cipher is. However, this also means that the slower the encryption & decryption. The block cipher will only provide computational secrecy, it means that it is not impossible to break the cipher, it is just very expensive. If the time and cost of attacks by using brute-force(when the cipher is secure) exceed the value or the useful lifetime of protected data, the attacker will be unlikely to attack.

Stream Ciphers: One-time Pad

Stream Cipher, different from block cipher, is easy and efficient, it is suitable to use in some situations like video meetings, audio transmitting and other real time scenarios. A image below shows the basic structure of One-time Pad cipher: 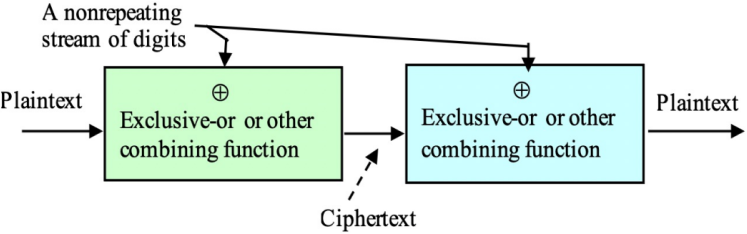The input plaintext is processed by Exclusive-or with a non-repeating stream of digits, the math expression could be: $$ciphertext (C) = plaintext (M)\ xor\ keystream (KS)$$

In stream cipher, the key must have the length of the plaintext, and we need as many possible keys as possible plaintext, and every key is equally likely. If there exists a reused key, it means the cipher is no more secure, this is because $$M1\ xor\ K = C1, M2\ xor\ K = C2$$ and this results in: $$M1\ xor\ M2 = C1\ xor\ C2$$ Moreover, if the attacker holds the set of ${ M1, C1 }$, the K is equals to $M1\ xor\ C1$

Therefore, to deal with this problem, we could replace the random generated keys by a pseudo-random sequence, which generated by a cryptographic pseudo-random generator that is “seeded” with the key.

Modes of Encryption

If a message is longer than a block size, block cipher can be used in a number of ways/modes to encrypt the message, in this blog we will introduce three of them, which these modes have been standardised internationally and are applicable to any block ciphers, which is ECB, CBC and CTR.

ECB - Electronic Code Book Mode

ECB mode is the most basic mode. In this mode, we use the same key to encrypt every blocks one by one, and we use the last byte to indicate the number of padding added. The math equation is like this:

Encryption: $$C_n = E_K(M_n)\ (or E(K, M_n))$$ Decryption: $$M_n = D_K(C_n); n = {1, 2, …}$$

For this mode, if we use the same plaintext to do encryption, the ciphertext will be exactly the same because we use the same key. And because of we encrypt the blocks one by one, reordering ciphertext blocks results in correspondingly reordered plaintext blocks. But the good thing is, errors in one ciphertext block only affects the same plaintext block, they do not propagate to other blocks.

CBC - Cipher Block Chaining Mode

The CBC mode is quiet similar to RNN neural network, where we use the encryption of last block into the next block encryption. 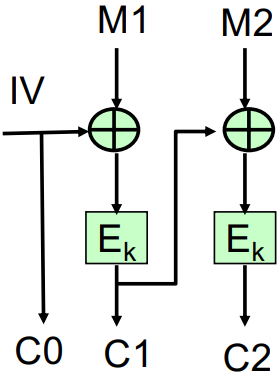We use the encryption result to add in the next encryption process, for the first encryption process we have a initial vector $C_0$, which is randomly selected and doesn’t need to be secure. The math representation is as below: $$C_i = E_K(M_i\ xor\ C_{i-1})$$

CTR - Counter Mode

The idea of CTR mode is to use a block cipher encryption function as the pseudorandom number generator to generate the key stream. We use this key stream, plus a counter value, which equals to the block size, being initialized with some value and plus 1 for each subsequent block(modulo 2n, where n is the block length), to do the encryption(xor operation) with plaintext. The structure is shown below:

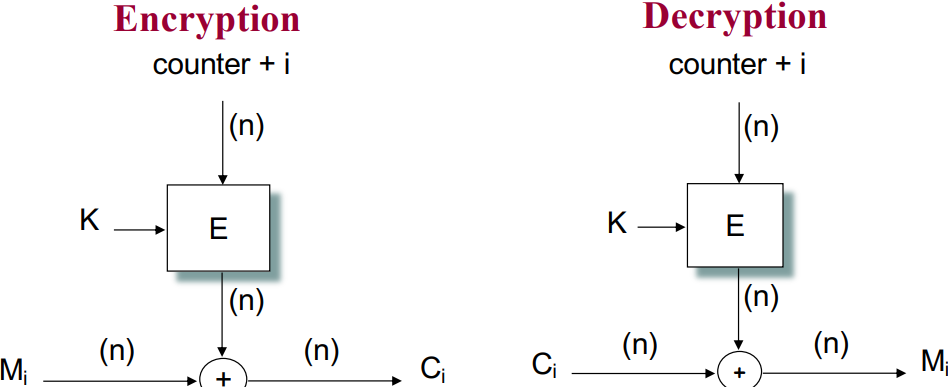
Actually, the CTR mode actually converts a block cipher into a stream cipher. Each of the block is processed independently, that means we are able to access the blocks randomly, the error caused by modifying a block during transmission won’t affect other blocks, and the blocks’ processes are parallelisable. One thing needs to mention is that the counter needs to be synchronized, if a block is inserted into or deleted from the ciphertext stream then synchronization is lost and the plaintext cannot be recovered.

Block Cipher VS. Stream Cipher

Block Cipher	Stream Cipher
Encrypt blocks of characters	Encrypt individual characters
Slower	Faster
Requires more memory space	Requires less memory space
	limited or no error propagation
	built without of block ciphers

Implementation Flaws

Here are some tips about some known vulnerabilities in software implementations:

1. Should use a secure random function from a crypto library. For example, rand() function in C should’t be use for security-critical applications.
2. IVs should be random

---

• ← Previous Post
• Next Post →