In this article we will have a look at POS tagging, what is it? How do we apply it to NLP tasks?
POS
POS - “Part of Speech”, represent a linguistic category, defined the syntactic or morphological behavior of words. “Traditional” categories contains 8 tags, they are:
- verb
- None
- Adverb
- Adjective
- Interjection
- Pronoun
- Preposition
- Conjunction
The previous 5 categories are called the open word classes, which means that these types always have a large amount of vocabularies and new words could be added into these categories. And the last 3 categories are called closed word classes, they doesn’t acquire new words to add in because most of them are used for building the text structure and connecting words or sentences, which has a limit number of vocabularies.
Another two notions of the word categories are content words and functional words. Content words define those words which take the responsibilities of demonstrating the meaning of a sentence, such as noun, verbs and adjectives, and most of them will vary in different form based on the tense alternation. Functional words define those words serving to express the grammatical relationships in text within a sentence, they usually doesn’t have much lexical meaning.
POS Tagging
After introduce POS, we could have a look wht is POS tagging, how to do it in steps and why it helps in nlp applications? So POS tagging means assigning POS to each words in the corpus. The example is shown below:

Why POS tagging is it useful? It is because of that, the same words in the corpus could have different POS tags depending on the context, which resolve lexical ambiguities. Here’s an example:
I can come tomorrow (Auxiliary)
I open the can (Noun)
We can beans in our factory (Verb)
POS Tag Prediction
There are two cues for doing the prediction of a tag, the internal cues (within the word) are morphology (on particular affixes), for example, -ous is often for adjectives and -ed is often for verbs. And the external cues are the contexts of the word. For example, in the sentence “I will read a book”, the tag for “book” could be predict by “a”, because “a”, as a DT (Determiner) often follows a noun.
POS Taggers
There are different type of POS tagger being developed, here are three types of them:
- Rule-based taggers
- Stochastic taggers
- Transformation taggers
Rule-based taggers
The rule-based taggers always start with a dictionary stores every possible tags for each words in the corpus, and during the tagging process, it selectively removes tags based on rules and finally leaving the correct tag.
Stochastic taggers
The key idea of stochastic taggers is to find, what is the best sequence of tags corresponds to this sequence of words? To answer this question, stochastic taggers considers all possible sequence of tags and choose the most probable one. In math language, we want to find the following equation:
$$\hat{t}_1^n = \underset{t_1^n}{\mathrm{argmax}} \ P(t_1^n\ |\ w_1^n)$$
argmax means the maximum value over all items
Hat(^) means “our estimate of the best one”
According to Bayes rule, the equation could be transform and simplify.
$$\hat{t}_1^n = \underset{t_1^n}{\mathrm{argmax}} \ P(t_1^n\ |\ w_1^n) = \underset{t_1^n}{\mathrm{argmax}} \ \frac{P(w_1^n\ |\ t_1^n)P(t_1^n)}{P(w_1^n)}$$
As $P(w_1^n)$ is the probability of the given sequence of words appear in the corpus, it doesn’t affect the result because we focus on the effect of different POS tags and this is a const for any sequence of tags. Therefore we are able to remove it, and the equation becomes:
$$\hat{t}_1^n = \underset{t_1^n}{\mathrm{argmax}} \ P(w_1^n\ |\ t_1^n)P(t_1^n)$$
Now, the equation contains two parts - $P(w_1^n\ |\ t_1^n)$ and $P(t_1^n)$, the first part is the likelihood, where given the sequence of tags and we could see the sequence of words. The second part is prior, which is the probability of the sequence of tag. For the likelihood, if we assume every words are independent to each other, it can be approximately equal to:
$$P(t_1^n) \approx \prod_{i=1}^{n} P(w_i | t_i)$$
And for the prior, transformation could be made by using chain rule, the varied form is as below:
$$P(w_1^n | t_1^n) \approx \prod_{i=1}^{n} P(t_i | t_{i-1})$$
Combining every steps we take above, the final equation could be:
$$\hat{t_1^n}= \underset{t_1^n}{\mathrm{argmax}} P(t_1^n\ |\ w_1^n) \approx \underset{t_1^n}{\mathrm{argmax}} \prod_{i=1}^{n} P(w_i\ |\ t_i)P(t_i\ |\ t_{i-1})$$
Now, the question become how do we get the value for both likelihood and prior? We could use the count-based estimation introduced in the last blog to solve this problem. The equations are:
Likelihood: $$P(w_i\ |\ t_i) = \frac{C(t_i, w_i)}{C(t_i)}$$
Prior: $$P(t_i\ |\ t_{i-1}) = \frac{C(t_{i-1}, t_i)}{C(t_{i-1})}$$
Transformation taggers
The Transformation tagger is based on TBL(Transformation-Based Learning), it contains three stages. In the start stage, it give a simple solution to the problem, and in iteration stage, it apply transformations(including rules automatically induced from training data) to get the best result. Finally TBL reaches stop stage when no more improvements could be made.
Brill POS tagger is an implementation of transformation taggers, below is a picture showing the steps of Brill POS tagger, we’ll introduce all it steps.
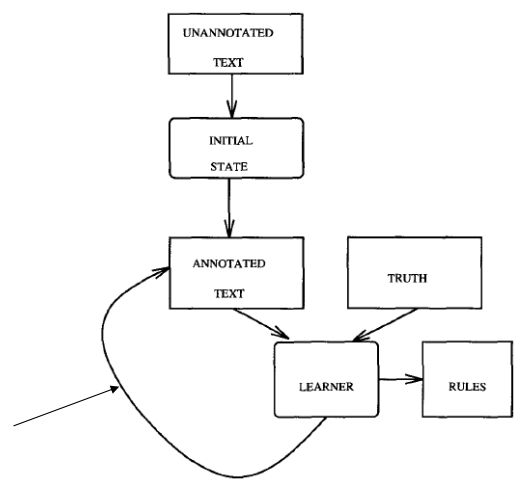
Initial Tagging
In the initial tagging, we tag all the words with its most likely tag, which are extracted from a tagged corpus. However there will be errors which need to fix it by transformations.
Transformations
In this stage, the tagger learn multiple rules, which could be separate into two types: non-lexicalized and lexicalized. The difference between these two types is that, non-lexicalized are external cues, and vice versa.
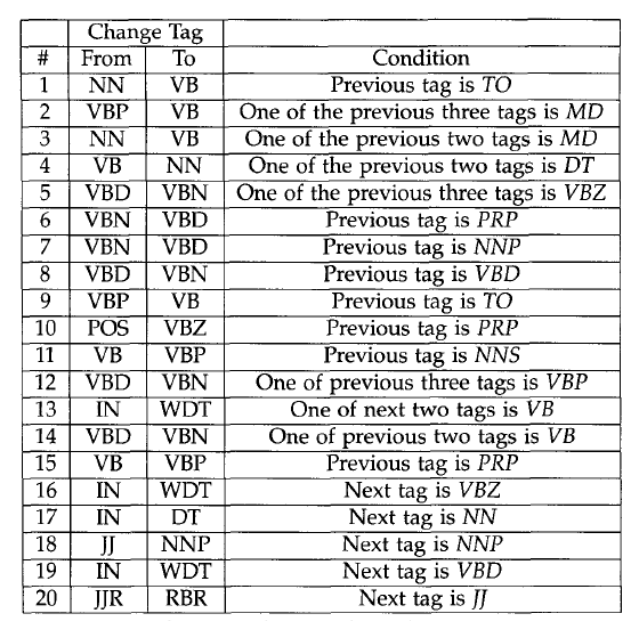
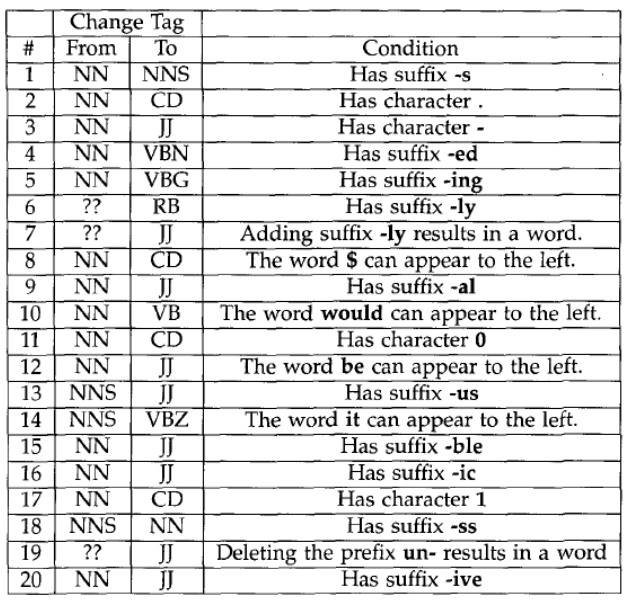
Tagging
Once all the rules are learned, we apply them to the corpus to get the final result.
POS Evaluation
We could use accuracy to measure for POS tagging, typically, the accuracy could reach 96% to 99%. Or, we could use error rate on particular tags or words, we could create a confusion matrix to demonstrate.