Algorithm and Data Structure - Turing Machine

In this article, we are going to look at the formal definition of Turing Machine and the therom with it.

Introduction of turing machine

The picture below is a multi-tape turing machine

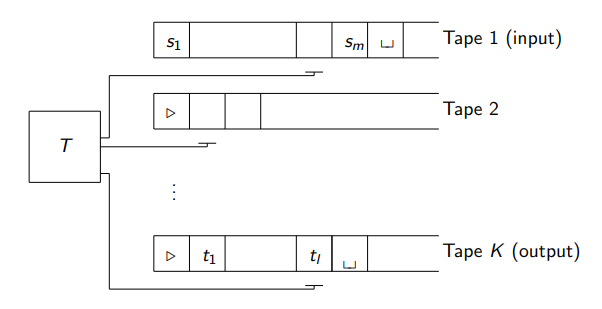
Definition

In a formal definition, a turing machine could be define as a quintuple:

M = [ K, Σ, Q, q0, T ]

K ≥ 2 (number of tapes)
Σ is a non-empty, finite set (alphabet)
Q is a non-empty, finite set (set of states)
q0 ∈ Q (initial state)
T is a set of transitions (for K, Σ and Q)

Symbol

A symbol is an element of 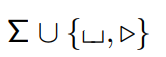which means blank and start separately.
We denote the set of finite strings over Σ by Σ∗

Transition

A transition is also a quintuple:

[ p, s¯, q, t¯, d¯ ]

p ∈ Q and q ∈ Q
s¯ and t¯ are K-tuples of symbols
d¯ is a K-tuple whose elements from {left, right, stay}

An informal explanation of transition is:

If you are in state p, and the current node being scanned is s¯, then set the new state to be q, write the symbol of t¯ on the tape and move as what d¯ says.

Here are few rules that a Turing Machine must follows:

The tape never moves to the left of start symbol.
Tape one is read-only and the last tape (K tape) is write-only.
the start symbol doesn’t involves in the transition
nothing is over-written with blank

Configuration

A Configuration is a set of snap shots of the turing machine which successive ones could form some transitions T, and a run of turing machine could be defined as a sequence of configurations. Formally, a configuration is a K-tuple of String, σ1 … σk, where each σ represents one element in the form:

start symbol, sk,1, ... , sk,i−1, q, sk,i, ... , sk,n(k)

This states that the head is currently at position i, where sk,i-1 is not scanned yet, and the current state is q.

if some transition is possible in a configuration of the run, then this is not the last configuration.
If the run is finite, then the turing machine is terminating
A deterministic turing machine M means, there is at most one transition T for each p and s¯. M ↓ x shows a deterministic turing machine is terminating with input x, and M ↑ x is non-terminating.

Here’s a therom:

Let M be a deterministic Turing machine over alphabet Σ, and let x ∈ Σ∗. If M ↓ x, then the output tape of M will contain a definite string y >∈ Σ∗; and we can define the partial function fM : Σ∗ → Σ∗ as follows.

fM(x) = if M ↓ x then y else undefined

In this case M computes the function fM. A partial function f : Σ∗ → Σ∗ is computable if it is computed by some (deterministic) Turing machine.

Encoding

A turing machine could be encoding into digits (prime power encoding). If we encode a turing machine M with code m, then we could input m;x(input x to a encoded turing machine m) to other turing machines.

Definition:

Define a turing machine U, a turing machine M over alphabet Σ with code m, and strings x, y ∈ Σ∗. U is terminating on input (m;x) with output y if and only if M is terminating on input x with output y. This also work with non-terminating.

More Definition (I hate it as well):

Acceptance: Define a turing machine M with input x ∈ Σ. M accepts x means M has a halting run with the first head over the leftmost square. In this case, x is recognized by M (recognition).

Even more definition (Dear god):

If a language is recognized by some Turing machine M, then it is recognized by some deterministic Turing Machine M’.
A language is recursively enumerable (simplified as r.e.) if there is a deterministic turing machine which recognizes it.
A language L over alphabet Σ is co-recursively enumerable (simplified as co-r.e.) if Σ∗ \ L is r.e.
A language is recursive if and only if it is both r.e. and co-r.e.

Decision Problem & Decidable Problem

A decision problem is some problem which has a yes or no answer in some language, and a recursive problem is some problem which test whether a decision problem is decidable (possible to give an answer).

We represent decision problems in this form: An example of this kind of problem could be: To decide whether a number is a prime number.

And an example of recursion problem is (Halting problem): This is an undicidable problem. Here’s the prove (First appear in 1936):

Suppose we have a turing machine H which, for every deterministic turing machine M with an x as its input, H returns yes if M ↓ x and no if M ↑ x. In another words, we have a turing machine which could solves the halting problem! Here we define another turing machine H*, it has a structure like this picture:

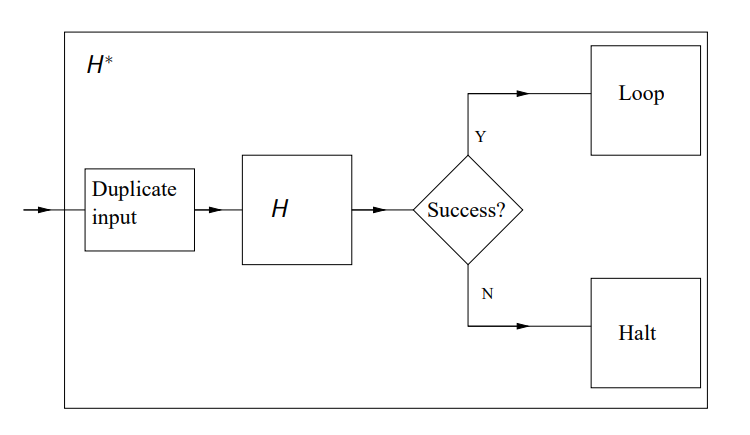
It takes an input to H. If H returns yes, then H* goes to a loop never ends. And if no, H* halts. Now, if H* take the code h* (which is itself) as the input, we will have two results.

If H returns a yes (H halts on h*), H* goes to the loop never ends, H* never halts.
If H returns a no (H doesn’t halt on h*), H* halts.

These two results are two paradox which proves that, the H we defined will never exist, so the Halting problem is a undecidable problem!